

Next: Energy
Up: Metallic cohesion
Previous: Quasi-Classical Description
Accordingly, the slow spatial variations require the substitution
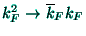 in (15), where
in (15), where
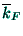 may be viewed as a variational parameter, the whole spatial variation
being transferred upon the new Fermi wavevector
may be viewed as a variational parameter, the whole spatial variation
being transferred upon the new Fermi wavevector 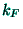 ; a similar
substitution
; a similar
substitution
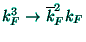 holds for the
electron density (14), and it is worth noting that such substitutions
are valid over those space regions where
holds for the
electron density (14), and it is worth noting that such substitutions
are valid over those space regions where
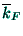 and
and 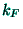 are
comparable in magnitude; such substitutions are corrected by the quantal
effects of the Hartree equations, as discussed above, as due to the abrupt
spatial variations of the self-consistent potential and the electron density
in the neighbourhood of the ionic cores. A linearized version[1] is
thereby obtained for the Thomas-Fermi scheme, which consists in
are
comparable in magnitude; such substitutions are corrected by the quantal
effects of the Hartree equations, as discussed above, as due to the abrupt
spatial variations of the self-consistent potential and the electron density
in the neighbourhood of the ionic cores. A linearized version[1] is
thereby obtained for the Thomas-Fermi scheme, which consists in
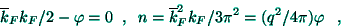 |
(17) |
according to (14) and (15), where the Thomas-Fermi screening
wavevector 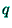 has been introduced through
has been introduced through
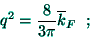 |
(18) |
it will be taken as the variational parameter; the Bohr radius
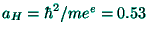 Å is used as length unit and the atomic unit
Å is used as length unit and the atomic unit
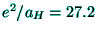 eV is also used for energy. Poisson's equation (7) reads now
eV is also used for energy. Poisson's equation (7) reads now
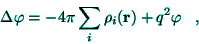 |
(19) |
and its solution provides the self-consistent field 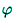 . It is worth
noting that the quasi-classical description and the quasi-classical
equilibrium equation (15) are valid for slow spatial variations,
requiring thus the linearized Thomas-Fermi scheme; the usual ''
. It is worth
noting that the quasi-classical description and the quasi-classical
equilibrium equation (15) are valid for slow spatial variations,
requiring thus the linearized Thomas-Fermi scheme; the usual ''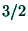 ''-Thomas-Fermi model, where
''-Thomas-Fermi model, where
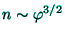 , would be inappropriate
for the slightly inhomogeneous electron liquid; the ''
, would be inappropriate
for the slightly inhomogeneous electron liquid; the '' ''-Thomas-Fermi
model holds in the classical limit of the quantal mechanics, which is often
called the ''quasi-classical approximation''.[2]
''-Thomas-Fermi
model holds in the classical limit of the quantal mechanics, which is often
called the ''quasi-classical approximation''.[2] [4]
[4]
Two-cluster aggregation
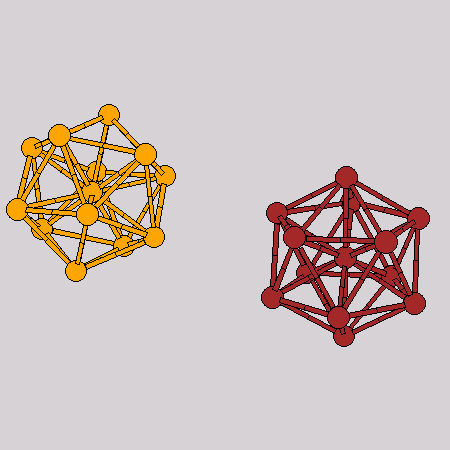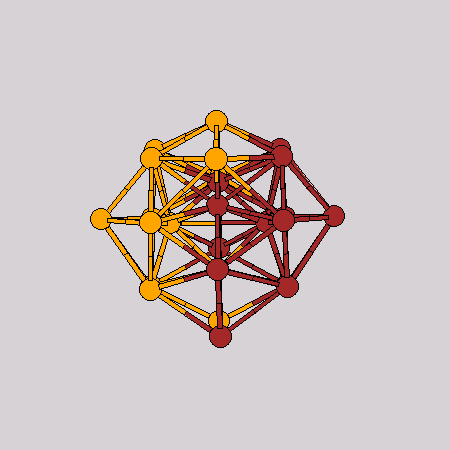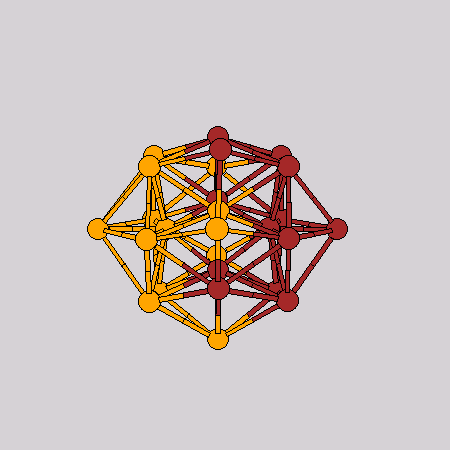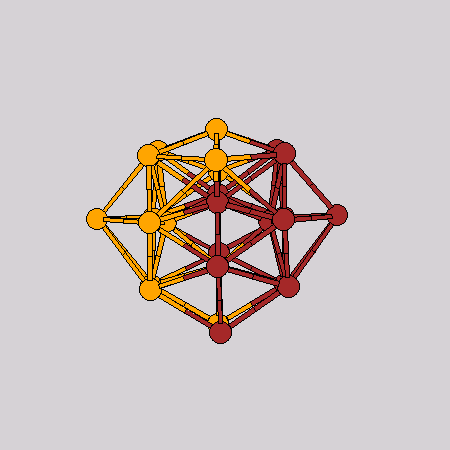
|
In order to estimate the effect of the quantal corrections, as
arising from those spatial regions of abrupt variations, the variational
parameter
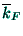 given by (18) (associated with the
electron density) may be compared with the average Fermi wavevector
given by (18) (associated with the
electron density) may be compared with the average Fermi wavevector
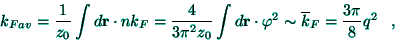 |
(20) |
where
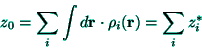 |
(21) |
is the total charge; it is worth noting here the electric neutrality of the
aggregate, as obtained from Poisson's equation (7), for instance; such
a comparison can also be made between the variational parameter 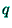 and the
average parameter
and the
average parameter  , obtained through (18) with
, obtained through (18) with
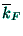 replaced by
replaced by 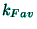 .
.


Next: Energy
Up: Metallic cohesion
Previous: Quasi-Classical Description

![]() given by (18) (associated with the
electron density) may be compared with the average Fermi wavevector
given by (18) (associated with the
electron density) may be compared with the average Fermi wavevector