Polarizability and Diamagnetic Susceptibility

An external electric field ${\bf E}$ produces an additional potential $-{\bf Er}$, and a change $\delta n$ in the equilibrium electron density; since $\int \delta n=0$, the kinetic energy (22) does not change, while the potential energy (23) gives

$$-\frac{4\pi }{q^{2}}n\delta n-\frac{1}{2}\varphi _{c}\delta n+{\bf Er}%% n=0\;\;\;,$$ (51)

and

$$\delta n=\frac{q^{2}}{4\pi }\frac{\varphi }{\varphi +\varphi _{c}/2}{\bf Er}%% \;\;;$$ (52)

the net change in energy is therefore

$$\delta E=-\frac{q^{2}}{4\pi }\int d{\bf r}\left( \frac{\var... ...+\varphi _{c}/2}\right) ^{2}\left( {\bf Er}\right) ^{2}\;\;;$$ (53)

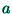hence one can get the electric polarizability.[1]$^{,}$[2] For a uniforrmly distributed nuclear charge $Nz^{*}$ in a sphere of radius $R$, one may use $\varphi =4\pi z^{*}/q^{2}a^{3}$ and $\varphi _{c}=2\pi z^{*}R^{2}/a^{3}$, where $a$ is the average inter-ionic distance; the change in energy is $\delta E=-[16/15(aq)^{2}]a^{2}R\left\vert {\bf E}\right\vert ^{2}$, and the polarizability $\chi _{e}=\left[ 32/15(aq)^{2}\right] a^{2}R$; as expected it vanishes for large $R$.

The electrons in a uniform magnetic field ${\bf H}$ have a diamagnetic energy

$$\delta E=-\frac{e^{2}}{8mc^{2}}\sum_{\alpha }\overline{({\bf H}\times {\bf r}%% _{\alpha })^{2}}\;\;\;,$$ (54)

where $c$ is the light velocity; hence,

$$\delta E=-\frac{e^{2}H^{2}}{12mc^{2}}\sum_{\alpha }\overlin... ...-\frac{e^{2}H^{2}}{12mc^{2}}\int d{\bf r}\cdot r^{2}n\;\;\;,$$ (55)

and, with a uniform distribution of nuclear charges, one obtains[1]$%% ^{,}$[2] $\delta E=$ $=-(\pi e^{2}/15mc^{2})(z^{*}R^{5}/a^{3})\left\vert {\bf H}\right\vert ^{2}$; the diamagnetic susceptibility is therefore $\chi _{d}=-(2\pi e^{2}/15mc^{2})(z^{*}R^{5}/a^{3})\simeq -0.54\cdot 10^{-4}\cdot (2\pi /15)(z^{*}R^{5}/a^{3})a_{H}$.